
These functions have the “smoothest” type of continuity, followed by uniform continuity and then plain old continuity. In other words, absolute continuity identifies which functions can be antiderivatives: a function on a closed, bounded interval is absolutely continuous on that interval if it is also an antiderivative over that same interval. Assuming the limit exists, “continuity at an endpoint” means that the function is continuous from the right (for the left endpoint) or continuous from the left (for the right endpoint).Ībsolutely continuous real-numbered functions are those functions for which the Fundamental Theorem of Calculus (FTC) holds.
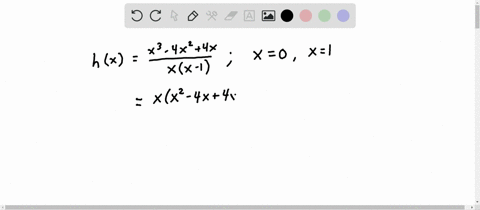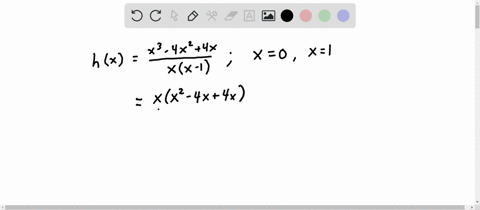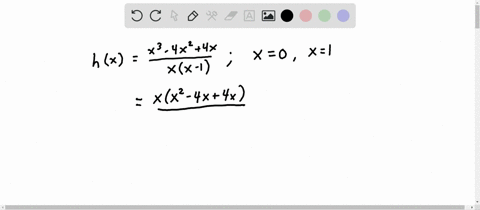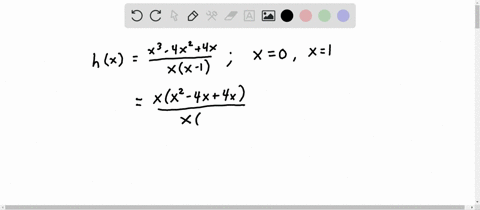
Continuity at an endpoint: There are two possible endpoints for a function: all the way to the left (in the far negative direction), and all the way to the right (in the far positive direction).As long as the function is continuous in that little area, then you can say it’s continuous on that specific interval. For example, you could define your interval to be from -1 to +1. Continuous on an interval: A function f is continuous on an interval if it is continuous at every point in the interval.However, sometimes a particular piece of a function can be continuous, while the rest may not be. the set of all real numbers from -∞ to + ∞). If a function is simply “continuous” without any further information given, then you would generally assume that the function is continuous everywhere (i.e. an airplane) needs a high order of continuity compared to a slow vehicle.

For example, modeling a high speed vehicle (i.e. Which continuity is required depends on the application. Modeling with Order of ContinuityĬontinuity in engineering and physics are also defined a little more specifically than just simple “continuity.” For example, this EU report of PDE-based geometric modeling techniques describes mathematical models where the C 0 surfaces is position, C 1 is positional and tangential, and C 3 is positional, tangential, and curvature. There are two “matching” continuous derivatives (first and third), but this wouldn’t be a C 2 function-it would be a C 1 function because of the missing continuity of the second derivative. For example, let’s say you have a continuous first derivative and third derivative with a discontinuous second derivative. Note here that the superscript equals the number of derivatives that are continuous, so the order of continuity is sometimes described as “ the number of derivatives that must match.” This is a simple way to look at the order of continuity, but care must be taken if you use that definition as the derivatives must also match in order (first, second, third…) with no gaps.

C2 FunctionĪ C 2 function has both a continuous first derivative and a continuous second derivative. C1 FunctionĪ C 1 function is continuous and has a first derivative that is also continuous. This simple definition forms a building block for higher orders of continuity. More specifically, it is a real-valued function that is continuous on a defined closed interval. C0 FunctionĪ C 0 function is a continuous function. Order of continuity, or “smoothness” of a function, is determined by how that function behaves on an interval as well as the behavior of derivatives. Order of Continuity: C0, C1, C2 Functions



 0 kommentar(er)
0 kommentar(er)
